"In 1999 a woman in the UK, Sally Clark, was convicted of murdering her two children. They had both seemingly died from SIDS (more commonly known as cot death), an unexpected but natural cause of death.
One of the main pieces of evidence against her was the testimony of a Professor and expert on child-abuse. He used the probability of one child (in a family with no known factors that might increase the chance of SIDS) dying of SIDS (1 in 8543). He then squared this fraction to get the probability of BOTH children dying from SIDS being about 1 in 73 million.
The jury saw this number as the probability of an innocent explanation and, since it was so low, found her guilty of the murders. Unfortunately the professor who testified was not an expert on probability and miscalculated. The jury also did not understand the meaning of the statistic being calculated and drew the wrong conclusions from it.
In this series of lessons we will look at why this probability of 1 in 73 million is both wrong and irrelevant to the case. We will also look at how probability could have been properly used in this case."
This is the introduction to a series of lessons on probability.This case will frame the students' work on probability throughout the unit and not one student will ask "when am I ever going to use this?"
There are many options on how open or closed a project this is. Because I was short on time (being interviewed) I first asked them if they could spot any problems in the probability (useful for showing progression) before working in quite a closed manner, as a class, through section 1**.
Section 1 - Improbable events never happen
Introduce expected frequency of events. After students understand the general concept and are able to calculate the expected frequency of different events. Get them to work on the questions below:The probability that both babies in a family of two will die of cot-death is 1/73'000'000.
There are about 340 million families with two children in the world.
1) How many families would you expect both babies to die of cot-death?
The probability of winning the lottery is 1/14'000'000.
About 7.5 million people play the lottery each week
2) How many winners would you expect to get:
i) Each week
ii) Each month
iii) Each year
iv) In 10 years
The probability of being born with 11 fingers or toes is 1/500.
3) What other information do you need to estimate the number of people in Bristol who were born with 11 fingers or toes?
4) Look at your answer to question 1. How is it related to the court case mentioned earlier? Does the answer to question 3 help you decide whether the woman was innocent or guilty?
5) Since the probability that both babies in a family of two will die naturally is 1/73'000'000, does that mean that the probability that both were murdered is 72'999'999/73'000'000? Explain why/why not?
I then got students to discuss question 4 in pairs before sharing with the group.
Concepts to get across:
- Probability is an estimate of frequency and whether something will happen or not depends a lot on the number of trials.
- Probability can not say for certain whether she is guilty or not as unlikely events do happen (though we can't be sure that's what happened here).
- The 73 million outcomes will include mostly families where neither child has died or a single child has died.
You could also go in to relative frequency here. This may help students understand where the 1 in 8543 statistic might have come from.
Section 2 - Dependent and Independent Events
Here you need to go in depth about the difference between dependent and independent events. Pupils need to be able to distinguish between the two, have some understanding about how the outcome of one event can change the probability of other events (e.g. if it rains today I am less likely to hang my washing out) and how to draw a probability tree from conditional probability problems.What does this have to do with the case? Well, the probability of 1 in 8543 can only be squared if the death of the two children are independent events (otherwise the probability of the second death would be a different fraction). The causes of SIDS is not entirely known, but it is highly plausible that there could be genetic or environmental factors that would be common to the two children. This would mean that if there were a SIDS death in a family, then further SIDS deaths would be more likely than otherwise.
Students can work on these questions to see this in action*:
1a. The probability that a family's first baby will die of cot-death is 1/8543.
If the first baby dies of cot-death, the probability that the second will also die of cot-death is 1/442.
If the first baby DOES NOT die of cot-death, the probability that the second will die of cot-death is 1/11002.
Draw a probability tree to show this information.
b. What is the probability that:
i. Neither child dies of cot-death?
ii. One of the children die of cot-death?
iii. Both children die of cot-death?
c. Using the number of families in the world with two children from the previous lesson (340 million), calculate how many families would you expect both babies to die of cot-death?
d. Why might the probability that the second child will die of cot-death be affected by whether the first child has also died of cot-death?
Section 3 - Further Conditional Probability
Now we get in to Bayes' theorem and the real reason why the 1 in 37 million statistic is simply irrelevant to the case:As seen in question 5 from section one, the probability of 1 in 73'000'000, even if it were correct, is not the probability of innocence. It would instead be the probability that if you picked any random family of two children, both children would have died AND the cause of death was cot-death. This is not appropriate to use in this case because we already know that both children died.
Again, pupils could first work on standard conditional probability questions until they are comfortable with the function and usage of the above formula. Then pupils are going to calculate the probability that both children have died of cot-death GIVEN that both children have died. They can also compare this to the probability that both children were murdered GIVEN that both children have died:
The probability that both children in a family of two will be murdered is 1 in 10 million.
1. What is the probability that both children will die of cot-death OR murder (use the probability calculated in the previous session).
2. What is the probability that both children have died of cot-death given that both children have died of EITHER cot-death OR murder?
2. What is the probability that both children have been murdered given that both children have died of EITHER cot-death OR murder?
3. How do these two probabilities compare?
4. How does this change your view of the case?
5. Does this help you decide whether the woman was innocent or guilty? How?
Wrapping it up
A great way to recap all of this would be to get the students to prepare a letter to send to the judge of the case explaining the ways in which probability has been misused in this case and in what ways the calculations could be improved upon.What is particularly great about this is that when they are done you can compare their letters to the letter written by the The Royal Statistical Society voicing their concerns (here) or the more specific letter written by Professor A.P. Dawid (of the R.S.S.) for her (successful) appeal (here)
Comments and Thoughts
*Although many of the figures used above are directly from the court case, and some are estimates based on other data I was able to find online, some of the data is currently unavailable and therefore is made up and should be used purely for illustration purposes.**How I would prefer to run it:
- Start each class recapping previous work and ideas on the case
- Introduce the topic of the lesson and work on standard questions of that topic
- Ask students: "how this topic might be related to the case? What data would we need to apply today's skills to this case?"
- Give them the data they ask for and let them do the calculations.
- Ask students: "How does this new information change your view of the case? Does this help you decide whether the woman is innocent or guilty? Why?"
There are many other problems with the probability used in the case including (but definitely not limited to):
- Some environmental factors were included in the calculation, which make the probability of cot-death less likely, but many other factors in this individual case (which could increase the risk of cot-death) were not included.
- Cot-death is not the only alternative cause of death to the theorised double-murder, but the probability of these other causes of death were not included.
- The study where the 1 in 8543 figure came from was not intended for use in a criminal trial and instead is looking at possible causes of cot-death. It does not, therefore, directly apply to this case.
I thought for some time about the ethics of using a real, living person's tragedy as the basis for a Maths lesson. However, since this particular miscarriage of justice is due solely to the misunderstanding of basic probability by many of the involved parties, its use to encourage a better understanding of this topic seems appropriate. I wouldn't want to involve this in a quick and easy pseudo-context question. Instead it should be handled with the importance and gravitas it deserves.
Here are some other links about this case:
- Wikipedia
- UnderstandingUncertainty.org
- Berkeley University - This one is my favourite. Though it is more complex than some of the others, it has a lot more information about the lack of data in some areas and the assumptions that need to be made in order to make the calculations work. Interestingly, this paper argues that the probability of double-murder is much higher (over 99%) than stated in any of the letters endorsed by the R.S.S. (the point still stands, however, that statistics, if used in court at all, should be verified and reviewed by professionals).
- Bad Science
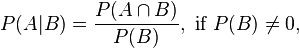


No comments:
Post a Comment